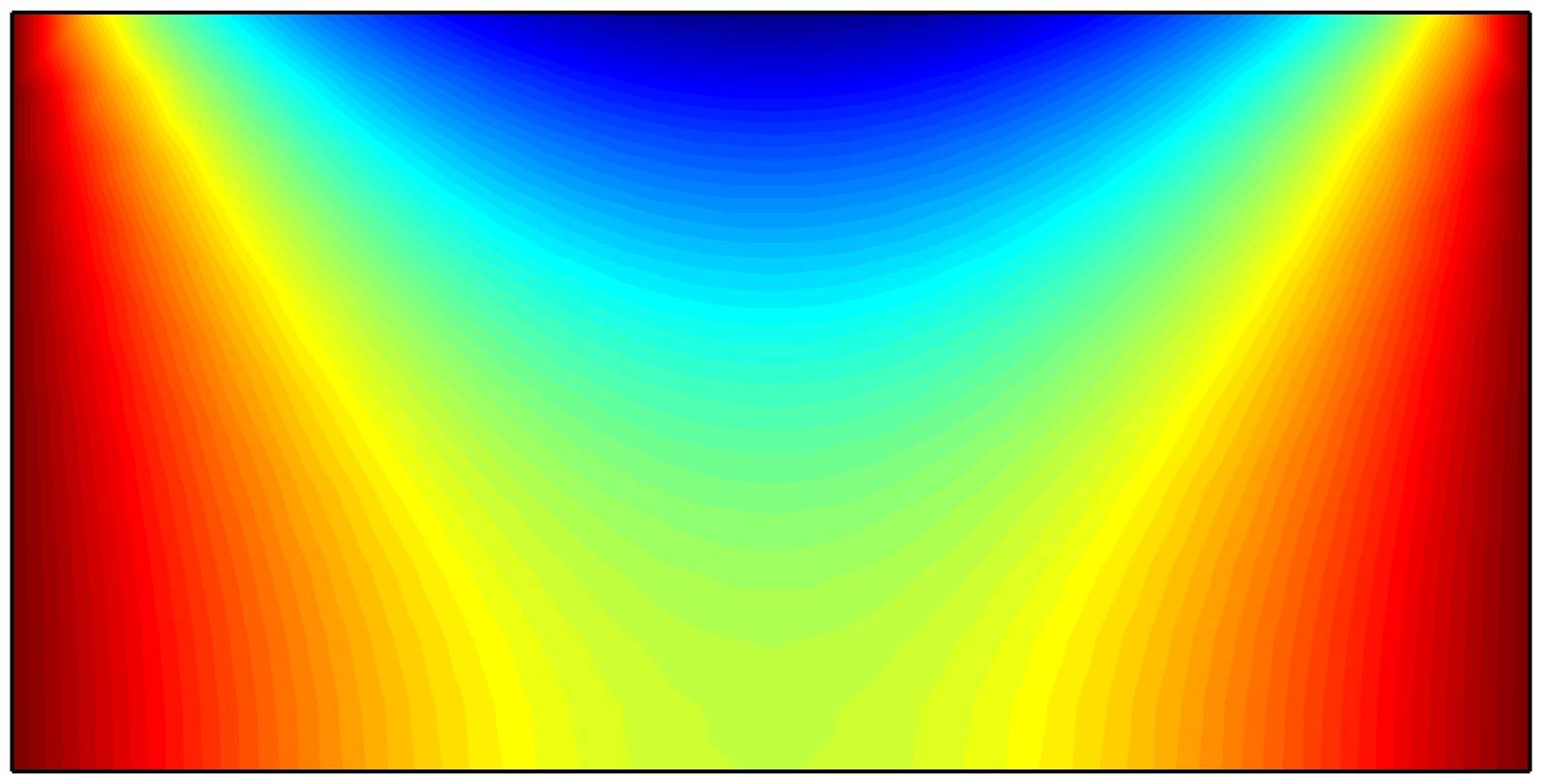
Flow in Driven Cavity
Stationary and laminar incompressible flow in a square cavity (Reynolds number, Re = 1000). The top of the cavity is prescribed a tangential velocity while the sides and bottom are defined as no-slip zero velocity walls. This model is available as an automated tutorial by selecting Model Examples and Tutorials… …
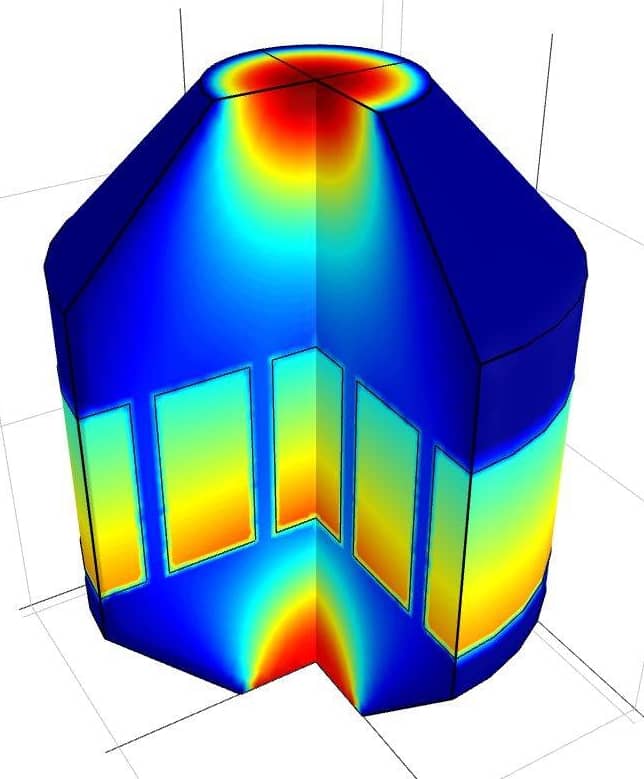
Flow in Porous Media
Axisymmetric laminar fluid flow in a diffusor duct or reaction chamber blocked by sections of a porous material. The model features several partially active subdomains with the Brinkman equations governing the fluid flow. The flow field with and without the porous material is compared. This model is available as an …
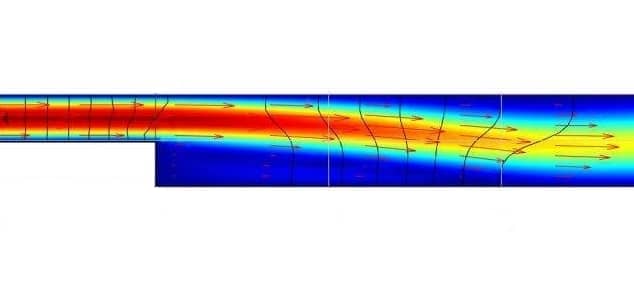
Flow Over a Backwards Facing Step
Flow over a backwards facing step is a classic computational fluid dynamics test problem which is used extensively for validation of simulation codes. The test problem essentially consists of studying how a fully developed flow profile reacts to a sudden expansion in a channel. The expansion will cause a break in the …
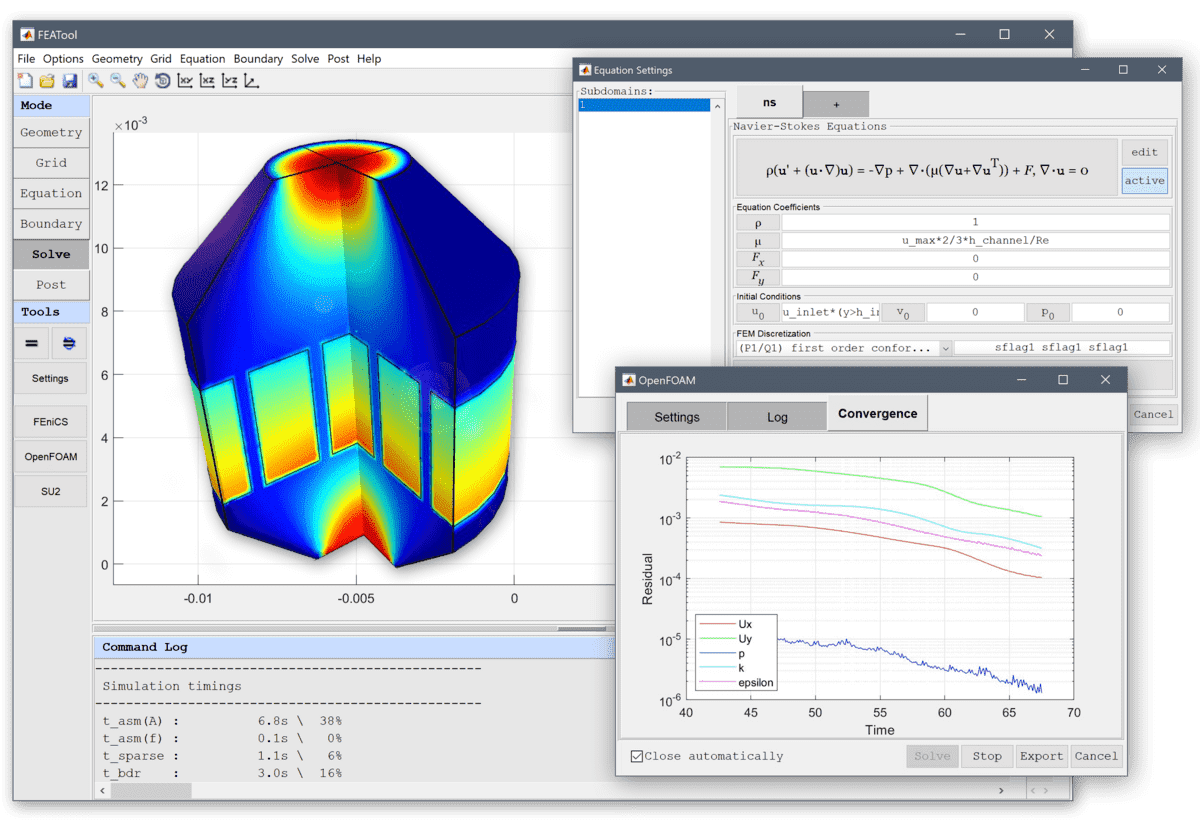
Heat Exchanger
This heat exchanger example illustrates the multiphysics modeling capabilities of FEATool. The model consists of a series of heated pipes surrounded by a fluid at a lower temperature, and features effects of both free and forced convection. Two types of physical phenomena are considered, fluid flow which is modeled by …
Heat Transfer in a Ceramic Strip
Two dimensional heat transfer of a ceramic strip with both radiation and convection on the top boundary. The ceramic has a thermal conductivity of 3 W/mK and the sides are fixed at a temperature of 900 °C while the bottom boundary is insulated. The surrounding temperature is 50 °C. The top boundary is exposed to both …
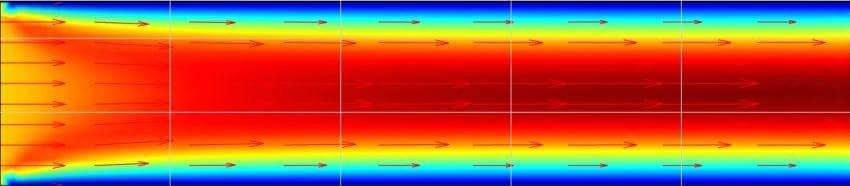
Laminar Channel Flow
Stationary and incompressible laminar Poiseuille flow in a two- dimensional rectangular channel. With a constant inflow profile u(0,y) = Umax and fixed no-slip walls, a fully developed laminar parabolic profile, u(y,L) = Umax4/h2y(h-y) is expected to develop at the outflow. This model is available as an automated …
Magnetic Field Around a Permanent Magnet
Example of simulation and visualization of the two-dimensional static magnetic potential field around a u-shaped permanent magnet. This model is available as an automated tutorial by selecting Model Examples and Tutorials… > from the File menu. Or alternatively, follow the linked step-by-step instructions. …
Poisson Equation
The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up in many applications (for example fluid flow, heat transfer, and chemical transport). It is therefore fundamental …
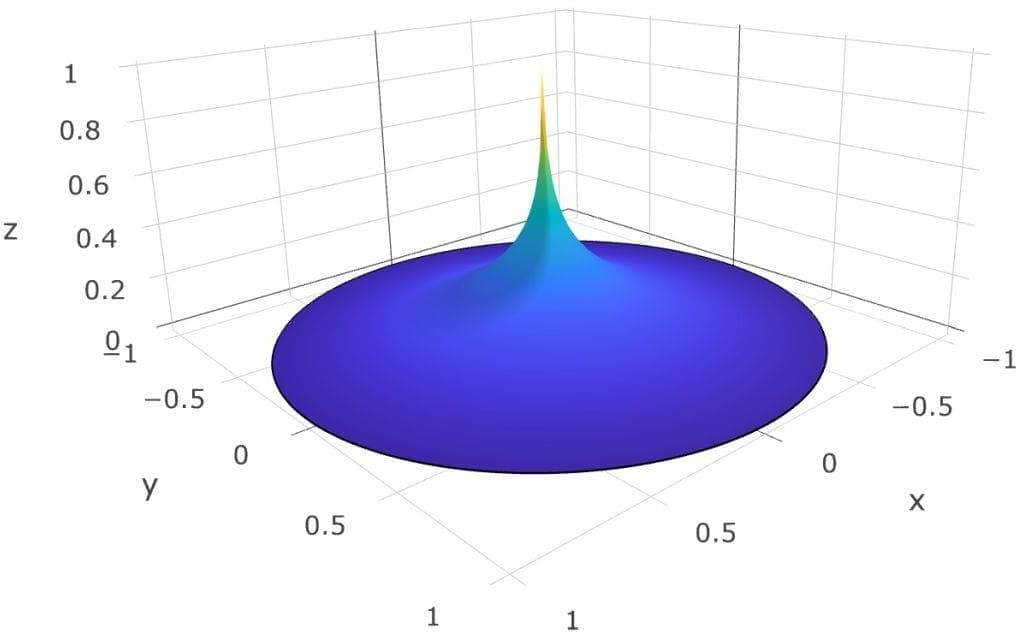
Poisson Equation with a Point Source
The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up again and again in many applications such as in fluid flow, heat transfer, and chemical transport. This example …
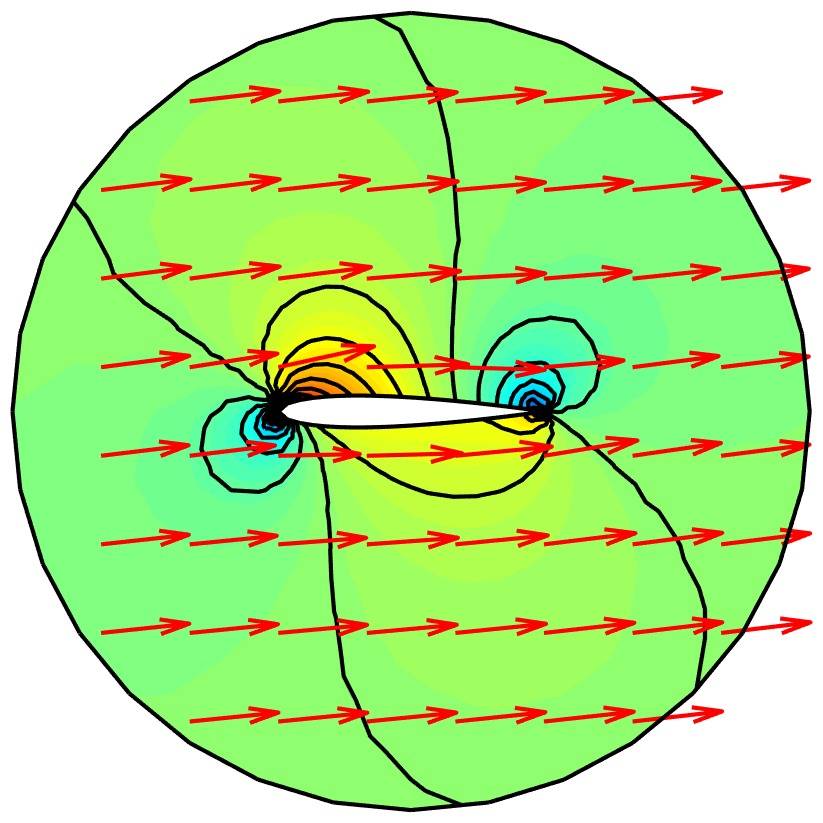
Potential Flow Over an Airfoil
This example models and simulates the flow field around the cross section of a NACA airfoil using the inviscid potential equation. The potential field is here modeled with the classic Laplace PDE equation with a correction for the discontinuity at the trailing edge (the Kutta condition). On the boundaries, there is …