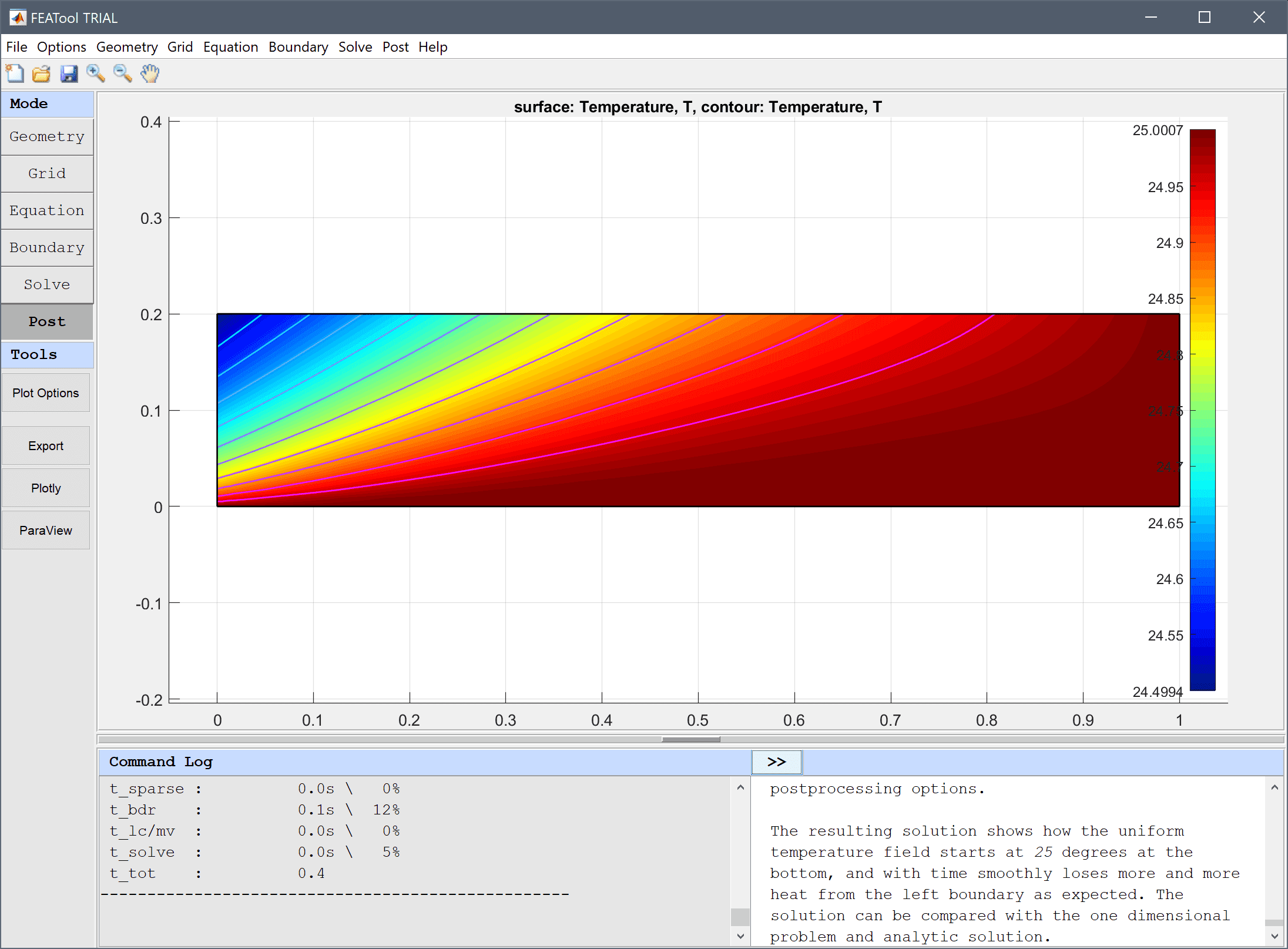
This example considers transient heat diffusion in a solid 1 m rod where one end is kept at T = 25 degrees and the other subject to constant heat flux q_n = 1. This one-dimensional time dependent problem is transformed to a static two dimensional one.
The computed results can both be compared with the analytical solution
$$ T_{ref} = (24+x) + \sum_{n=1}^\infty 8/(1-2n)^2/\pi^2cos((n-1/2)\pi x)e^{-((n-1/2)^2\pi^2)t}$$
and the equivalent one dimensional heat transfer in a rod example.
This model is available as an automated tutorial by selecting Model Examples and Tutorials… > Heat Transfer > Space-Time Transformation of Heat Conduction from the File menu, and also as the MATLAB simulation m-script example ex_heat_transfer8. Step-by-step tutorial instructions to set up and run this model are linked below.