The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up again and again in many applications such as in fluid flow, heat transfer, and chemical transport.
This example shows how to up and solve the Poisson equation
$$ d_{ts}\frac{\partial u}{\partial t} + \nabla\cdot(-D\nabla u) = f $$
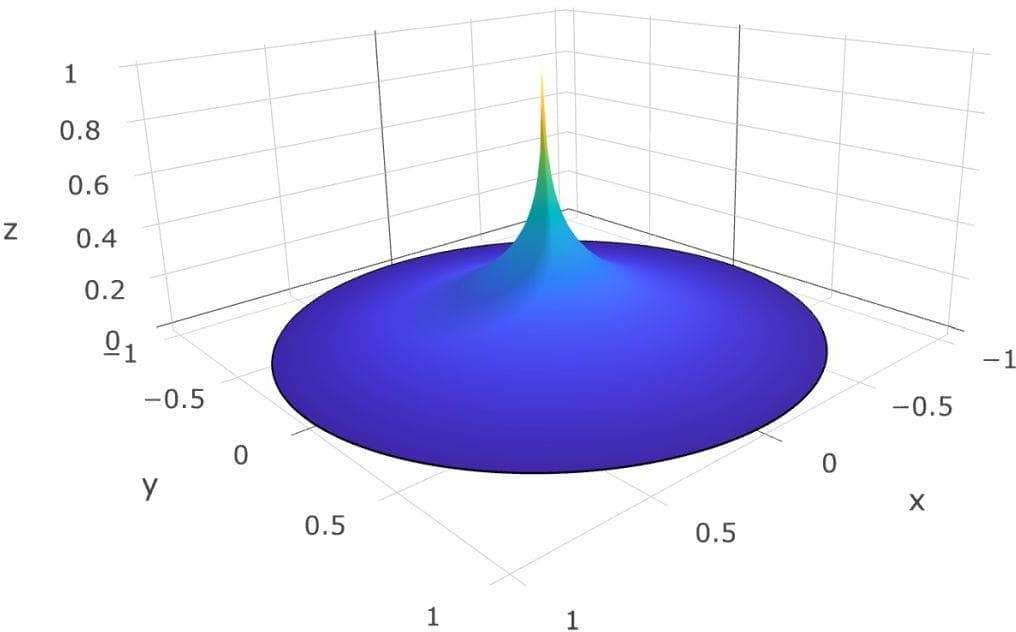
for a scalar field u = u(x) on a circle with radius r = 1. The diffusion coefficient D = 1 and right hand side source term f = δ(0) which prescribes a point source at the center. The Poisson problem is also considered stationary meaning that time dependent term can be neglected. With these assumptions the equation simplifies to
$$ - \Delta u = \delta(0,0) $$
Moreover, homogeneous Dirichlet boundary conditions are prescribed on all boundaries of the domain, that is u = 0 on the boundary. The exact solution for this problem is u(x,y) = -1/(2π)log( r ) and can be used to measure the accuracy of the computed solution.
This model is available as an automated tutorial by selecting Model Examples and Tutorials… > Quickstart > Poisson Equation with a Point Source from the File menu, and is also available as the MATLAB simulation m-script example ex_poisson7. Or alternatively, follow the linked step-by-step tutorial and video instructions.