Gmsh Mesh Generator
Gmsh is a very capable and cross platform stand-alone open source mesh generator for FEA and CFD applications. In addition to many built-in mesh generation algorithms, it also includes support for a variety of integrated mesh generators, such as Tetgen and Netgen, and also popular 2D and 3D CAD file formats such as STEP, IGES, and STL. As such is it one of the most flexible and popular mesh generators, and can be used with FEATool Multiphysics from the fully integrated GUI as well as MATLAB® scripting and programming API.
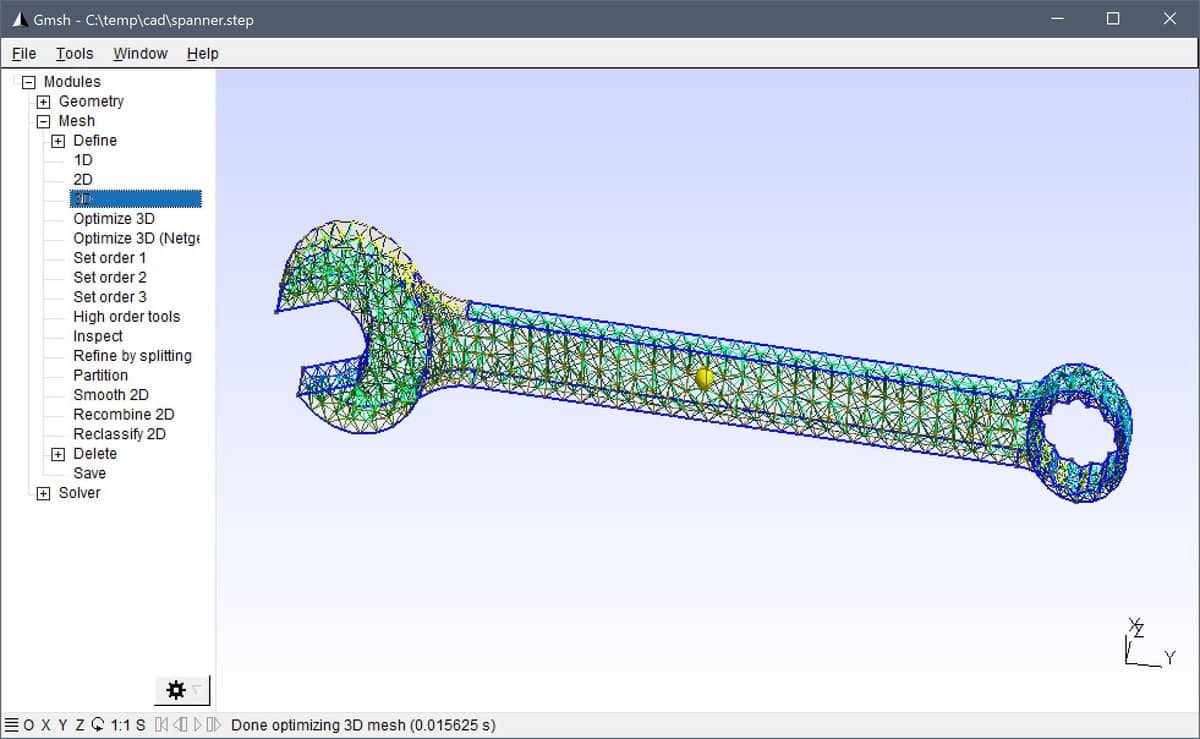
Some advantages of using Gmsh compared to the other grid generators is robustness and mesh generation speed (primarily for 3D geometries). Moreover, Gmsh also supports better and more control with a selection of different mesh generation algorithms, and specifying the grid size in different geometry regions, subdomains, as well as on boundaries, allowing for greater flexibility and better grids tuned for the specific problems and geometries. In addition, Gmsh also supports generating boundary layers and unstructured quadrilateral grids which can be useful for fluid dynamics simulations.
Gmsh with the FEATool GUI
Gmsh Installation
Before processing, first ensure that the latest FEATool Multiphysics version is installed (as a MATLAB toolbox Add-On if you wish to use Gmsh with MATLAB).
When using the FEATool Multiphysics toolbox, the Gmsh executable will be automatically downloaded and installed when required. If the Gmsh installation fails, please manually download and install Gmsh from the homepage [1] (any of Gmsh versions 3.0.6, 4.3.0, and 4.5.2 are recommended, as they have been tested and validated for use with the FEATool toolbox).
Gmsh with MATLAB GUI
Once installed, the Grid Generation Settings dialog box will in 2D and 3D feature a Gmsh selection option from the Grid Generation Algorithm drop-down box. Moreover, the following options also apply to the Gmsh mesh generation algorithm
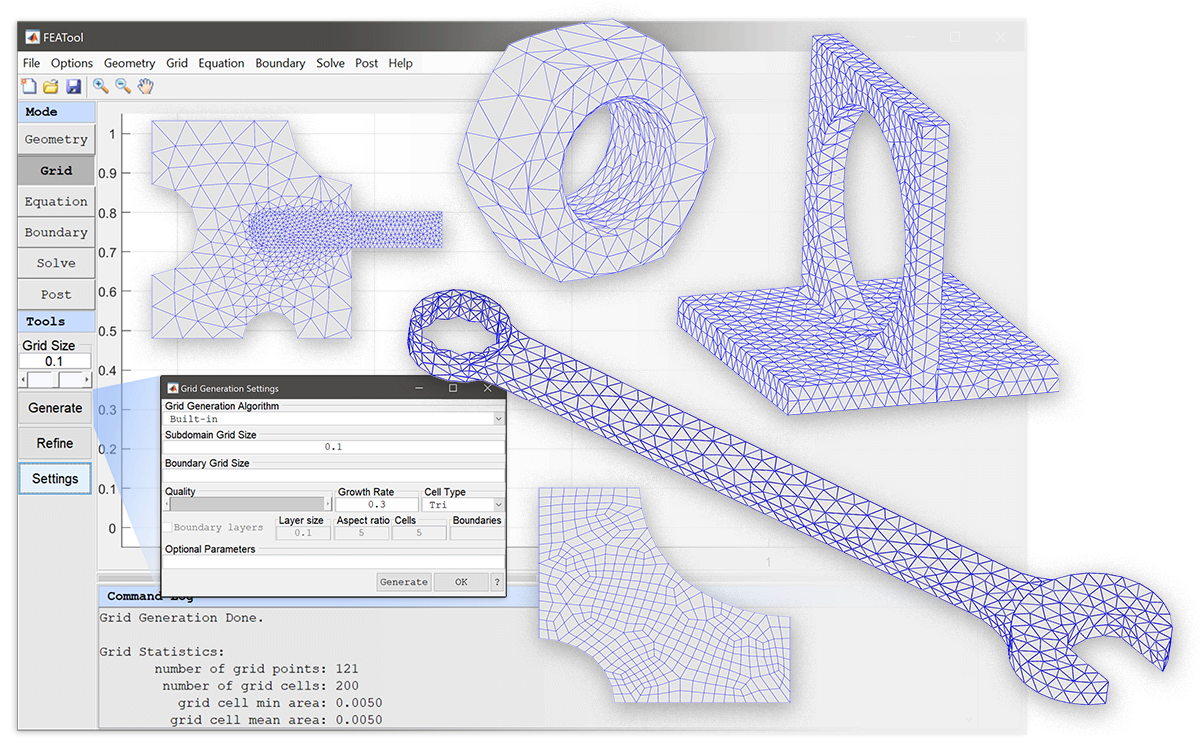
The Subdomain Grid Size, hmax, indicates the target grid cell diameter, and can either be a single scalar prescribing the grid size for the entire geometry, or a space separated string of numbers (array) where the hmax values correspond to the generated subdomains.
Boundary Grid Size, hmaxb, is analogous to hmax but related to boundaries (edges). hmaxb can consist of a single scalar applicable to all boundaries, for example
0.1prescribing a mean cell edge length of 0.1 on every boundary. hmaxb can also be a numeric array with entries corresponding to individual boundaries, for example
0.1 0.2 0.3 0.4specifying cell edge length 0.1 for boundary 1, 0.2 for boundary 2 etc.
The Smoothing parameter specifies the number of post grid smoothing steps to perform (default 3).
Selecting the Internal Boundaries check-box in 2D enables mesh generation of structured boundary layers on boundaries. The height of the boundary layer can be specified with the Layer Size and also Aspect Ratio between cells. With Gmsh it is also possible to specify the number of mesh Cells in the boundary layer, and the boundary numbers to apply boundary layer generation to.
In 2D one can also choose between Triangular and Quadrilateral Cell Types.
The Generate grid button effectively calls the gridgen command line function from the GUI, which in turn makes a system call to Gmsh, after which the generated grid is automatically imported and displayed.
MATLAB Gmsh Programming API
On the MATLAB command line the gridgen function is used to call Gmsh to generate unstructured 2D or 3D triangular grids. The following syntax is used
grid = gridgen( SIN, VARARGIN, 'gridgen', 'gmsh' )
where SIN is a valid FEATool fea model struct, geometry
definition struct, or cell array of geometry objects. The gridgen
function also accepts the following property/value pairs
(VARARGIN).
Property Value/{Default} Description
-----------------------------------------------------------------------------------
hmax scal/arr {0.1} Target grid size for geometry/subdomains
hmaxb scal/arr {[]} Target grid size for boundaries
nsm scalar {3} Number of grid smoothing steps
nref scalar {0} Number of uniform grid refinements
algo2 scalar {2} 2D mesh algorithm (1=MeshAdapt, 2=Automatic,
5=Delaunay, 6=Frontal, 7=BAMG, 8=DelQuad)
algo3 scalar {1} 3D mesh algorithm (1=Del, 2=New Del, 4=Front
5=Front Del, 6=Front Hex, 7=MMG3D, 9=R-tree)
blayer struct {[]} Data struct for Gmsh 2D boundary layers
quad boolean {false} Use quad meshing (for 2D)
tol scalar {eps*1e3} Deduplication tolerance
compound boolean {true} Use Gmsh compound boundaries
mshopt cell {} Cell array of Gmsh options
mshall boolean {true} Output/save all meshed entities
mshver integer {2} Gmsh msh file version (1/2/4)
nt integer {numcores/2} Number of concurrent threads
verbosity integer {5} Gmsh verbosity/output level
syscmd string {'default'} Gmsh system call command
(default 'gmsh fdir/fname.geo -')
fname string {'fea_gmsh_UID'} Gmsh imp/exp file name (root)
fdir string {tempdir} Directory to write help files
clean boolean {true} Delete (clean) Gmsh help files
instdir string {userpath/.featool} Gmsh binary installation directory
fid scalar {1} File identifier for output ([]=no output)
Among the properties hmax indicates target grid cell diameters, and is either a numeric scalar valid for the entire geometry or an array with hmax values corresponding to the subdomains. hmaxb is similar to hmax but a numeric array with a hmaxb values corresponding to the boundaries (including internal boundaries).
NSM (default 3) the number of post smoothing steps to perform. NREF (default 0) the number of post uniform grid refinement steps. ALGO2 and ALGO3 the Gmsh 2D and 3D mesh generation algorithms. QUAD (default 0) toggles Blossom-Quad conversion for 2D geometries.
Additional Gmsh options can be provided with the cell array MSHOPT. For example MSHOPT could be given as
{{'Mesh', 'CharacteristicLengthMax', '1'}, {'Mesh', 'AnisoMax', '10'}}
More detailed information regarding the mesh generation options can be found in the documentation for Gmsh. Also, for more information about CLI usage access the function help by entering
>> help gridgen
in the MATLAB command line interface.
MATLAB Mesh Generation Examples
The following section presents a few examples to illustrate how one can generate FEA and CFD meshes on the MATLAB command line, and in m-file scripts with the programming API.

Unit square with uniform global grid size set to 0.1.
grid = gridgen( {gobj_rectangle()}, 'hmax', 0.1, 'gridgen', 'gmsh' ); plotgrid( grid ) % Plot and visualize mesh.Unit square with fine grid along the top boundary.
grid = gridgen( {gobj_rectangle()}, 'hmax', 0.5, ... 'hmaxb', [0.5 0.5 0.01 0.5], 'gridgen', 'gmsh' ); plotgrid( grid )Domain with curved boundaries meshed with quadrilaterals.
geom.objects = {gobj_rectangle(), gobj_circle([0 0],.6), gobj_circle([1 1],.3,'C2')}; geom = geom_apply_formula( geom, 'R1-C1-C2' ); grid = gridgen( geom, 'hmax', 0.1, 'quad', true, 'gridgen', 'gmsh' ); plotgrid( grid )Two connected subdomains with refined grid along the shared boundary (9)
geom.objects = { gobj_polygon([-2e-3 -8e-3;0 -8e-3;0 -6e-3;0 6e-3;0 8e-3;-2e-3 8e-3]), ... gobj_polygon([0 -6e-3;2e-3 -5e-3;2e-3 4e-3;0 6e-3]) }; hmax = 5e-4; hmaxb = hmax*ones(1,4); hmaxb(9) = hmax/5; grid = gridgen( geom, 'hmax', hmax, 'hmaxb', hmaxb, 'gridgen', 'gmsh' ); plotgrid( grid )Composite component with several subdomains.
r1 = gobj_rectangle( 0, 0.11, 0, 0.12, 'R1' ); c1 = gobj_circle( [ 0.065 0 ], 0.015, 'C1' ); c2 = gobj_circle( [ 0.11 0.12 ], 0.035, 'C2' ); c3 = gobj_circle( [ 0 0.06 ], 0.025, 'C3' ); r2 = gobj_rectangle( 0.065, 0.16, 0.05, 0.07, 'R2' ); c4 = gobj_circle( [ 0.065 0.06 ], 0.01, 'C4' ); geom.objects = { r1 c1 c2 c3 r2 c4 }; geom = geom_apply_formula( geom, 'R1-C1-C2-C3' ); geom = geom_apply_formula( geom, 'R2+C4' ); grid = gridgen( geom, 'hmax', [0.0025 0.05 0.0025], 'gridgen', 'gmsh' ); plotgrid( grid )Complex geometry with several holes and subdomains.
w = 10e-4; L = 3*w; H = 5*w; p1 = gobj_polygon( [w/10 0;(L-w/4)/2 0;(L-w/4)/2 H;0 H;0 H/3], 'P1' ); p2 = gobj_polygon( [(L+w/4)/2 0;L 0;L H-H/3;L H;(L+w/4)/2 H], 'P2' ); r1 = gobj_rectangle( (L-w/4)/2, (L+w/4)/2, 0, H, 'R1' ); c1 = gobj_circle( [2*w/3 3*w], w/3, 'C1' ); c2 = gobj_circle( [2*w/3 2*w], w/3, 'C2' ); c3 = gobj_circle( [2*w/3 1*w], w/3, 'C3' ); c4 = gobj_circle( [L-w/2 4.5*w], w/8, 'C4' ); c5 = gobj_circle( [L-w 4.5*w], w/8, 'C5' ); c6 = gobj_circle( [L-w/2 4*w], w/8, 'C6' ); c7 = gobj_circle( [L-w 4*w], w/8, 'C7' ); c8 = gobj_circle( [L-w/2 3.5*w], w/8, 'C8' ); c9 = gobj_circle( [L-w 3.5*w], w/8, 'C9' ); c10 = gobj_circle( [L-w/2 3*w], w/8, 'C10' ); c11 = gobj_circle( [L-w 3*w], w/8, 'C11' ); geom.objects = { p1 p2 r1 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 }; geom = geom_apply_formula( geom, 'P1-C1-C2-C3' ); geom = geom_apply_formula( geom, 'P2-C4-C5-C6-C7-C8-C9-C10-C11' ); hmaxb = zeros(1,21); hmaxb([6 20]) = w/50; grid = gridgen( geom, 'hmax', w./[5 20 5], 'hmaxb', hmaxb, 'gridgen', 'gmsh' ); plotgrid( grid )
Notes
For geometries with multiple and overlapping geometry objects the actual subdomain numbering will generally not correspond to the geometry object numbering (two intersecting geometry objects will for example create three or more subdomains and several internal boundaries). In this case the actual subdomain and boundary numbering for vector valued hmax and hmaxb arrays can easiest be visualized and determined by first creating a coarse grid and switching to Equation/Subdomain and Boundary modes, respectively.
Gmsh propagates the hmax and hmaxb values down to the specific nodes in the mesh which means that it is currently not possible to exactly define mesh sizes for subdomains and boundaries.
Gmsh also generates temporary geo and msh data files which, if required, can be found in the directory specified by the fdir parameter (default given by the MATLAB tempdir command).
References
[1] Gmsh - A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities.
[2] Geuzaine C., Remacle J.-F. Gmsh: a 3D finite element mesh generator with built-in pre- and post-processing facilities, International Journal for Numerical Methods in Engineering 79 (11), pp. 1309-1331, 2009.